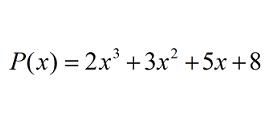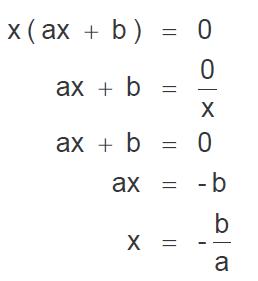LÓGICA MATEMÁTICAS
Método o razonamiento en el que las ideas o la sucesión de los hechos se manifiestan o se desarrollan de forma coherente y sin que haya contradicciones entre ellas.
PROPOSICION
Una
proposición es una unidad semántica que, o sólo es verdadera o sólo es falsa.La proposición es un elemento fundamental de la lógica matemática; se puede expresar
en oraciones.
ORACIONES QUE SI SON PROPOSICIONES:
1)Oraciones afirmativas.
Yo me llamo felipe (Informan).
2)Oraciones descriptivas.
Mi perro es color blanco(Describen).
3)Oraciones explicativas.
Si hoy es lunes mañana sera martes (Explican).
ORACIONES QUE NO SON PROPOSICIONES:
¡Auxilio, me ahogo! ORACION EXCLAMATIVA
No hables en clase ORACION IMPERATIVA
¿Qué día es hoy? ORACION INTERROGATIVA
No sé si vendrán al viaje. ORACION DESIDERATIVAS
VALOR DE VERDAD
El
valor de verdad de una proposición es la cualidad de veracidad que describe
adecuadamente la proposición. Este puede ser verdadero o falso..
CUANDO ES VERDAD:
1 - V - T - TRUE
a: Los dias de la semana son 7 ⬌ 1
b: yo me llamo Felipe Rosero ⬌ 1
CUANDO ES FALSO:
0 - 1 - F - FALSE
a: 10 > 9 ⬌ 1
b: 5 es un numero par ⬌ 1
TABLA DE VERDAD
Una tabla de verdad, o tabla de valores de verdad, es unatabla que muestra el valor
de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.
PROPOSICION
Una
proposición es una unidad semántica que, o sólo es verdadera o sólo es falsa.La proposición es un elemento fundamental de la lógica matemática; se puede expresar
en oraciones.
Una tabla de verdad, o tabla de valores de verdad, es unatabla que muestra el valor
de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.
Son símbolos que se usan para comparar dos valores. Si el resultado de la comparaci
ón es correcto la expresión considerada es verdadera, en caso contrario es falsa.
Por ejemplo, 8>4,

EJEMPLO.
- No te encontre en el cine
- Fui a la uniersidad y la biblioteca estaba cerrada
- Tienes el cabello largo o pequeño
- Si me voy a quito entonces te llevo
- Paso el pre si y solo si estudio mucho
Son símbolos que se usan para comparar dos valores. Si el resultado de la comparaci
ón es correcto la expresión considerada es verdadera, en caso contrario es falsa.
Por ejemplo, 8>4,
ón es correcto la expresión considerada es verdadera, en caso contrario es falsa.
Por ejemplo, 8>4,
EJEMPLO.
- No te encontre en el cine
- Fui a la uniersidad y la biblioteca estaba cerrada
- Tienes el cabello largo o pequeño
- Si me voy a quito entonces te llevo
- Paso el pre si y solo si estudio mucho
CONJUNCIÓN (^)
se
presenta con los términos gramaticales: “y”, “pero”, “más”, “también”,
“sin embargo”, “además” y signos de puntuacion como: la coma, el punto
y el punto y como.
Es verdad cuando p= ^ , q= ^ p^q= ^
 a: Me voy a milagro
b: luego a bucay
a^b: Me voy a milagro y luego a bucay
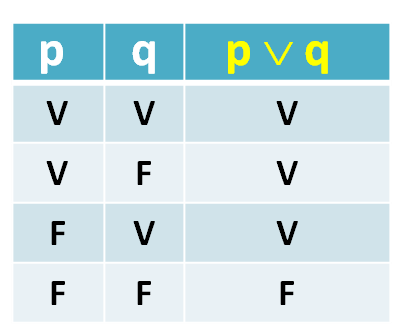
DISYUNCIÓN
(V)
Se presenta con el termino gramatical (o) como ejemplo es:
Es falso cuando p= F , q= F p v q= F
a: Hoy es viernes
b:Domingo
a v b: Hoy es lunes o domingo
a: Me voy a milagro
b: luego a bucay
a^b: Me voy a milagro y luego a bucay
DISYUNCIÓN
(V)
Se presenta con el termino gramatical (o) como ejemplo es:
Es falso cuando p= F , q= F p v q= F
a: Hoy es viernes
b:Domingo
a v b: Hoy es lunes o domingo
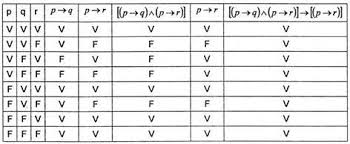
CONDICIONAL (➜)
Viene
a ser la combinación de dos proposiciones con “si… entonces”. Se
lee si
p entonces q.
Es falsa cuando, p=V , q=F P➜Q= F
a: Si estudio mucho
b: pasare a semestre
a ➜ b: Si estudio mucho entonces pasare a semestre
BICONDICIONAL.⬌
Se denomina doble inplicacion, se utiliza con el termino gramaticas (si y solo si).
Es verdad cuando p=V , q=V P ⬌ q=V
p=F , q=F P ⬌ q=F

a: Es 4
b: Sumados 2 mas 2
a ⬌ b: Es 4 si y solo si sumados 2 mas 2
a: Puedes tomar el vuelo
b: Compras un pasaje
a ⬌ b: Puedes tomar el vuelo si, y solo si, compras un pasaje,
CLASES DE PROPOSICIONES.
Las proposiciones se clasifican en:
- Proposicion simple
- Proposicion compuesta
PROPOSICION SIMPLE.
Son aquellas que no tienen oraciones componentes afectadas por negaci
ones ("no") o términos de enlace como conjunciones ("y"), disyunciones
("o").
EJEMPLO:
1) Lisbeth roxana es una pintora (Simple)
2) El 14 y el 7 son factores de (Simple)
3) El 2 o el 3 son divisores de 48. (Simple)
PROPOSICIÓN
COMPUESTA
Es una frase que consta de uno o varios sujetos y de un predicado que afirma
al entorno a dichos sujetos, es decir esta comformado por 2 o mas P.simples.
EJEMPLO:
1) Sen(x) no es un número mayor que 1. (Compuesta)
2) El 14 es factor del 42 y el 7 también es factor del 42. (Compuesta)
3) El 2 es divisor de 48 o el 3 es divisor de 48. (Compuesta)
Que es conjunto
CONJUNCIÓN (^)
se
presenta con los términos gramaticales: “y”, “pero”, “más”, “también”,
“sin embargo”, “además” y signos de puntuacion como: la coma, el punto
y el punto y como.
Es verdad cuando p= ^ , q= ^ p^q= ^
a: Me voy a milagro
b: luego a bucay
a^b: Me voy a milagro y luego a bucay
DISYUNCIÓN
(V)
Se presenta con el termino gramatical (o) como ejemplo es:
Es falso cuando p= F , q= F p v q= F
a: Hoy es viernes
b:Domingo
a v b: Hoy es lunes o domingo
CONDICIONAL (➜)
Viene
a ser la combinación de dos proposiciones con “si… entonces”. Se
lee si
p entonces q.
Es falsa cuando, p=V , q=F P➜Q= F
a: Si estudio mucho
b: pasare a semestre
a ➜ b: Si estudio mucho entonces pasare a semestre
BICONDICIONAL.⬌
Se denomina doble inplicacion, se utiliza con el termino gramaticas (si y solo si).
Es verdad cuando p=V , q=V P ⬌ q=V
p=F , q=F P ⬌ q=F
a: Es 4
b: Sumados 2 mas 2
a ⬌ b: Es 4 si y solo si sumados 2 mas 2
a: Puedes tomar el vuelo
b: Compras un pasaje
a ⬌ b: Puedes tomar el vuelo si, y solo si, compras un pasaje,
CLASES DE PROPOSICIONES.
Las proposiciones se clasifican en:
- Proposicion simple
- Proposicion compuesta
PROPOSICION SIMPLE.
Son aquellas que no tienen oraciones componentes afectadas por negaci
ones ("no") o términos de enlace como conjunciones ("y"), disyunciones
("o").
EJEMPLO:Son aquellas que no tienen oraciones componentes afectadas por negaci
ones ("no") o términos de enlace como conjunciones ("y"), disyunciones
("o").
1) Lisbeth roxana es una pintora (Simple)
2) El 14 y el 7 son factores de (Simple)
3) El 2 o el 3 son divisores de 48. (Simple)
2) El 14 y el 7 son factores de (Simple)
3) El 2 o el 3 son divisores de 48. (Simple)
PROPOSICIÓN
COMPUESTA
Es una frase que consta de uno o varios sujetos y de un predicado que afirma
al entorno a dichos sujetos, es decir esta comformado por 2 o mas P.simples.
EJEMPLO:
1) Sen(x) no es un número mayor que 1. (Compuesta)
2) El 14 es factor del 42 y el 7 también es factor del 42. (Compuesta)
3) El 2 es divisor de 48 o el 3 es divisor de 48. (Compuesta)
Es una frase que consta de uno o varios sujetos y de un predicado que afirma
al entorno a dichos sujetos, es decir esta comformado por 2 o mas P.simples.
EJEMPLO:
1) Sen(x) no es un número mayor que 1. (Compuesta)
2) El 14 es factor del 42 y el 7 también es factor del 42. (Compuesta)
3) El 2 es divisor de 48 o el 3 es divisor de 48. (Compuesta)
Que es conjunto
Un conjunto es la agrupación de objetos que encuentran relacionados o poseen una racterística comun.
Notacion de un conjunto:
- Los conjuntos se escriben entre llaves { }
- Denota mediante letras mayúscula.
- Sus elementos se separan mediante coma

- Por Extensión y tabulacion
- Por Comprensión
- Diagrama de Venn
POR COMPRENSION:
El conjunto esta compuesto por todos los numeros naturales mayores que 5.
NOTACION:B={ x/x ∈ N / x > 5 }
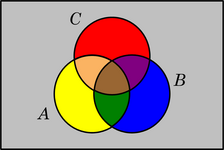
DIAGRAMA DE VENN
Consistente en dos o más áreas circulares que representan conjuntos de elementos que
tienen una característica común,que se interseccionan representar conjuntos de manera
gráfica mediante dibujos
Consistente en dos o más áreas circulares que representan conjuntos de elementos que
tienen una característica común,que se interseccionan representar conjuntos de manera
gráfica mediante dibujos
Ejemplo:
CARDINALIDAD DE UN CONJUNTO
Es la cantidad de elementos de un conjunto A. Se denota por el símbolo N(A).
Ejemplo:
Es la cantidad de elementos de un conjunto A. Se denota por el símbolo N(A).
Ejemplo:
A= {lunes, Martes. Miercoles,
Jueves, Viernes}
su cardinal
N (A) =5
su cardinal
N (A) =5
TIPOS
DE CONJUNTOS
·
Conjunto Vacío
·
Conjunto Unitario
·
Conjunto Finito
·
Conjunto Infinito
·
Conjunto Universo o Referencial
CONJUNTO VACÍO:
Es un conjunto que no tiene elementos, también se le llama conjunto nulo. Generalmente
se le
representa por los símbolos: f o { }
CONJUNTO UNITARIO
El conjunto unitario es
aquel que posee solamente un elemento.
Ejemplos:
El conjunto de números naturales mayores de 8
y menores de 10:
C = { 9 }
El único elemento es el número 9.

CONJUNTO FINITO
Un conjunto es finito, cuando posee un comienzo y un final, en otras palabras,
es cuando los elementos del conjunto se pueden determinar o contar.
Un conjunto es finito, cuando posee un comienzo y un final, en otras palabras,
es cuando los elementos del conjunto se pueden determinar o contar.
Ejemplos:
R = { 10,12,14,16,18,20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40 }
CONJUNTO INFINITO
El conjunto es infinito, cuando posee un inicio pero no tiene fin. Es decir, que la cantidad
de elementos que conforman el conjunto no se puede determinar.
Ejemplo:
de elementos que conforman el conjunto no se puede determinar.
Ejemplo:
N = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13,...}
CONJUNTO UNIVERSAL O REFERENCIAL
Es el que contiene todos los elementos que deseen considerarse en un
problema,
discurso o tema, sin pretender contener todo lo que no interesa al
problema.
Ejemplo:
A={x/x es letra de las palabras ecuador }
A={ e,c,u,a,d,o,r}
RELACION Y FUNCIONES

se trata de la correspondencia que existe entre dos conjuntos: a cada elemento del primer conjunto le corresponde al menos un elemento del segundo conjunto.
PRODUCTO CARTESIANO
De dos conjuntos es una operación, que resulta en otro conjunto,
cuyos elementos son todos los pares ordenados.
EJEMPLO:
CONJUNTO A={a,e,i} y B={1,2,3} N(AxB)={N(A)} {N(B)}
AXB={x,y/xEA y xEB} (3) x (3)= 9
AxB={(a,1),(a,2),(a,3)}
(e,1),(e,2),(e,3)
(i,1).(i,2),(i,3)
Se multiplican los elementos tanto de A y B
GRAFICO CARTESIANO
DOS CONJUNTOS RELACIONADOS
•En una relación binaria intervienen dos conjuntos, el primero se
llama «conjunto de partida» y el segundo «conjunto de llegada».
DOMINIO:
Es un subconjunto del conjunto de partida, formado por los elementos
que están relacionado, el dominio siempre a ser el conjunto de partida.
RANGO:
es un subconjunto del conjunto de llegada, formado por los elementos que
están relacionados,siempre va a estar en el conjunto de llegada.
REGLA DE CORRESPONDENCIA
Es una expresión que permite establecer una relación entre elementos
de los conjuntos. Algunos ejemplos son:
«es múltiplo de»
«trabaja en»
«es de nacionalidad»
«a+b=12»
«y = x-3»
RELACION
Sean A y B conjuntos. Un subconjunto R del producto cartesiano A × B se
P(A × B).
EJERCICIO GENERAL
Estudiemos el siguiente ejemplo: José, Ana y Luis tienen preferencia por Matemática; Ana, Raúl y Silvia tienen preferencia por Biología y Luis,
Carlos y Pedro tienen preferencia por Lenguaje e Historia; Omar no tiene
preferencia por ninguna materia.
A={jose,ana,luis,raul,silia,carlos.pedro.omar}
B={matematica,biologia,lenguaje,historia}
N(AxB)={N(A)} {N(B)}
8 4
AxB={(JM); (A,M); (A,B); (LM); (LL); (LH); (RB); (SB); (CL); (CH); (PL); (PH)}.
REPRESENTACION GRAFICA
DIAGRAMA SAGITAL:
REPRSENTACION GRAFICA


AxB={(JM); (A,M); (A,B); (LM); (LL); (LH); (RB); (SB); (CL); (CH); (PL); (PH)}.

FUNCIONES
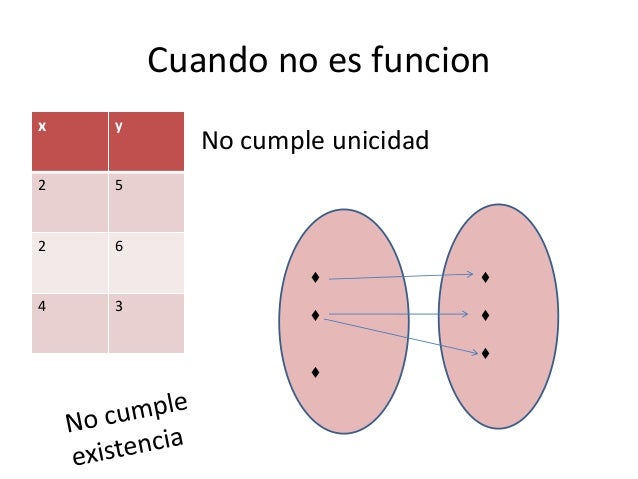
De otra si el valor de la primera depende del valor de la segunda.
Una relación debe cumplir 2 condiciones para ser función
Todo elemento del conjunto de partida X debe tener imagen.
Esta imagen debe ser única.
Toda función es relación, pero no toda relación es función.
Si es funcion:
No es funcion:

TIPOS DE FUNCIONES
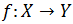


INYECTIVA:
Decimos que la aplicación
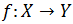
Es inyectiva si las imágenes de elementos distintos del dominio son distintas.
Dicho matemáticamente,

x={ 1,2,3} y={ D,B,C,A}
f={(1,D),(2,B).(3,A)
SOBREYECTIVA:
Decimos que la aplicación
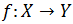 Es sobreyectiva (o suprayectiva) si todo elemento del codominio tiene anti-imagen. Es decir,
Es sobreyectiva (o suprayectiva) si todo elemento del codominio tiene anti-imagen. Es decir,
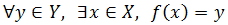
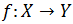 Es biyectiva si es inyectiva y sobreyectiva.
Es biyectiva si es inyectiva y sobreyectiva.
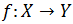
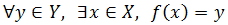
Sean los conjuntos x={1,2,3,4} y={D.B.C}
BIYECTIVA:
Decimos que la función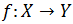
RELACION Y OPERACION ENTRE CONJUNTOS
CUANTIFICADORES
Existen tres tipos de expresiones son:
Verdadera 10=10
Falsa 9=12
Abierta 5x>4
Algo muy importante las expresiones abiertas pueden variar pueden ser erdaderas o
falsa.
falsa.
CUANTIFIADOR UNIVERSAL ➜∀
con una determinada propiedad Ejemplo.
∀x, 2x+3x = 5x
x=0 2(0)+3(0)=5(0)
x=1 0 + 0 = 0
0 = 0
cuantificador existencial ➜∃
Se usa para indiar que hay uno o mas elementos en el conjunto
A(no necesariamente unicos)
que cumplen una determinada propiedad se escribe.
∃x, 5x+2 = 4
5(1) +2=4
5+2=4
X=1 7=4 Es falso
SUBCONJUNTO ➔⊆
Un subconjunto se da cuando todos los elementos de un conjunto pertenece al otro.
Un conjunto de B es SUBCONJUNTO de un conjunto,A si B esta contenido dentro
de A.Por ejemplo, el conjunto de frutas rojas y el conjunto de frutas amarillas
de A.Por ejemplo, el conjunto de frutas rojas y el conjunto de frutas amarillas
subconjuntos del conjunto de frutas, puesto que todas las frutas rojas son frutas
, y todas las frutas amarillas son frutas también:
, y todas las frutas amarillas son frutas también:

SUBCONJUNTO PROPIO
Si el conjunto A es subconjunto del conjunto B, y por lo menos un elemento
de B no pertenece a A entonces se dice que A es subconjunto propio de B.
Ejemplo.
A={ x, y. z } B={ a, x, u }
A es subconjunto de B
CONJUNTOS IGUALES.
Se da cuando dos o mas conjuntos contienen iguales elementos por Ejemplo.
A= {x Є N / 3 < x < 10} = {4, 5, 6, 7, 8, 9}
CONJUNTO POTENCIA➜ P(A).
Es aquel que esta formado por todo los subconjuntos posibles de A ,y aquel
que esta formado por todos los subconjuntos que se encuentra en A
CARDINALIDAD DEL CONJUNTO POTENCIA
N(P(A) = 2N(A)
Ejemplo.
A={a, b, c }
N(P(A) =2N(A) = 2x2x2 = 8
P(A) = { ∅, {a}, {b}, {c},
{a, b}, {a,c},{b, c}, A}.
CONJUNTOS DISJUNTOS.
Son disjuntos si y solo si no tenemos elementos en comun , se dice que dos
conjunos A y B si no setiene ningun elemento en comun son disjuntos si su
interseccion es vacia.
conjunos A y B si no setiene ningun elemento en comun son disjuntos si su
interseccion es vacia.
Elemplo.
A={1, 2, 3, 4, 5 }
B={a,b,c,d,e}
CONJUNTOS INTERSECANTES.
Son aquellos que tienen elementos en comun entre A y B por lo menos un elemento en
comun, se llama asi por que su interseccion es un conjunto no vacio.
Ejemplo.
A={10,15,20,25,30,35,40,45}
B={3,6,9,12.15.18.21.24,27,30,45}
OPERACIONES CON CONJUNTOS.
UNION DE CONJUNTOS.➜U
cuyos elementos son los mismos de los conjuntos iniciales. Por ejemplo, el conjunto
de los numeros naturales es la unión del conjunto de los números pares positivos P
y el conjunto de los númerosimpares positivos
Ejemplo.
A={1-1.2.3} B={2,4,6}
A={1-1.2.3} B={2,4,6}
AUB={1,-1,2,3,4,6
INTERSECCION DE CONJUNTOS.➜∩
Es la cual se intersecta entre dos o mas conjuntos ,la intersección de dos (o más)
conjuntos es una operación que resulta en otro conjunto que contiene los elementos
comunes a los conjuntos de partida.
Ejemplo.
B={Luis,Ana,Ines,Beto}
N={Ana,Beto,Pedro}

DIFERENCIA DE CONJUNTOS.➜ –
La entre dos conjuntos es una operación que resulta en otro conjunto, cuyos
elementos son todos aquellos en el primero de los conjuntos iniciales que no
estén en el segundo.
estén en el segundo.
Ejemplo.
A={3,6,9,12 }
B={2,4,6,8,10,12 }
A - B ={3,9,}

COMPLEMENTEOS DE UN CONJUNTOS.➜A΄
Es otro conjunto que contiene todos los elementos que no están en el conjunto original.
Para poder definirlo es necesario especificar qué tipo de elementos se están utilizando,
o de otro modo, cuál es el conjunto universal.
o de otro modo, cuál es el conjunto universal.
Ejemplo.
RE={a,e,i,o,u }
A={e,i,o}
B={a,e,i,u}
A΄={a,u}
DIFERENCIA SIMÉTRICA DE CONJUNTOS.➜ Δ
Es una operación que resulta en otro conjunto cuyos elementos son aquellos que
pertenecen a alguno de los conjuntos iniciales, sin pertenecer a ambos a la vez.
Ejemplo.
CONJUNTO
DE LOS NÚMEROS

CLASIFICACION DE LOS NUMEROS


CLASIFICACION DE LOS NUMEROS

LOS NUMEROS REALES R
Los
números reales son los que abarcan a los números racionales y los números irracionales. Se lo representa con la letra:
CONJUNTOS NUMERICOS
NUMEROS RACIONALES. (Q)
Es todo número que puede representarse como el cociente dedos números enteros o, más precisamente, un entero y un natural positivo; es decir, una fracción común con numerador y denominador distinto de cero.
EJEMPLO.

Un número irracional es un número que no se puede escribir en fracción - el decimal sigue para siempre sin repetirse.
EJEMPLO.
√7 = 2,645751311064591
NUMEROS NATURALES.(N)
Los números naturales son aquellos que permiten contar loselementos de
un conjunto.
EJEMPLO.
N = {1,2,3,4,5.....}
NUMEROS ENTEROS. (Z)
Los números enteros abarca los números negativos incluyendo eL cero y los números
positivos. Y se representa.
EJEMPLO.
= {-3, -2, -1, 0, 1, 2, 3,
4, ….}




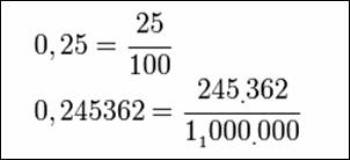




Polinomios iguales
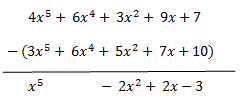

División de polinomios
Consiste en hallar uno de los factores de un producto, que recibe el nombre de cociente
dado el otro factor, llamado divisor, y el producto de ambos factores llamado dividendo.
EJEMPLO.

POR EL METODO DE RUFFINI

USO DE LA RAZON.

Es el conjunto formado por los
números enteros positivos, el cero y los números enteros negativos.
Divisores y Múltiplos
Si a, b, c ∈ Z cumplen la relación c
= a
. b,
entonces decimos:
üa
y b
son
factores o divisores de c
üc
es
múltiplo de a y b.
EJEMPLO:
10x10=100
- 20 es divisible para 2
- 12 es > que 15
Mínimo común múltiplo (m.c.m.)
Es el menor múltiplo común distinto de cero.Para hallar el mínimo común
múltiplo de dos o más números debemos de descomponer el número en
factores primos.
múltiplo de dos o más números debemos de descomponer el número en
factores primos.

Máximo Común Divisor (M.C.D.)
de dos o más número natural o enteros (no números con decimales) es el número
más grande que les divide.
más grande que les divide.

TIPOS DE NUMEROS DECIMAL
Para realizar,,basta
dividir el numerador por el denominador, obteniendo tres
tipos de números Decimales:
EJEMPLO:
tipos de números Decimales:
EJEMPLO:
üDecimales finitos (1,5; 2,4)
üDecimales infinitos periódicos
(0,55555….)
üDecimales infinitos semiperiódicos (4,2888..)
REPRESENTACION DECIMAL

TRANFORMACIÓN DECIMALES FINITOS
Se caracterizan por tener una
cantidad finita de dígitos después de la coma
decimal,hacia la derecha.
decimal,hacia la derecha.
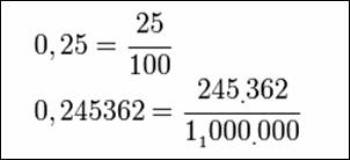
Se diferencia por tener uno o más dígitos que se repiten infinita

TRANSFORMACIÓN DECIMALES INFINITOS SEMIPERIÓDICOS
Se
caracterizan por tener una o más cifras antes del período, queforman
lo que denomina
el anteperíodo.
LEYES DE POTENCIAS
Todo numero elevado a 0 siempre va ser igual a 0

LEYES DE SIGNOS PARA POTENCIAS

JERARQUIA DE LAS OPERACIONES
ALGO MUY IMPORTANTE SE DEBE RESOLVER DE MAS INTERNO AL MAS
EXTERNO.

EJEMPLO:
Forma incorrecta
8 * 7 + 4
8 * 11 = 88
Forma
Correcta:
5 * 3+
3
15 + 3 = 18
EJERCICIO GENERAL
3²+8x2+6x3+4-9/3x5-7+2³
9+8x2+6x3+4-3x5-7+8
9+16+18+4-15-7+8
55-22
33
respuesta
(12-8)+4-(20-7x3)+8+20/5
(4)+4-(20-21)+8+20/5
4+4-(-1)+8+20/5
4+4+1+8+4
21
respuesta
25/5x4x2+5-(12+4x3)
25/5x4x2+5-(12+12)
25/5x4x2+5-(24)
5x4x2+5-24
4o+5-24
45-24
21
respuesta
Expresiones Algebraicas






Expresiones Algebraicas
Es
una expresión en la que se relacionan valores indeterminados con constantes y
cifras
NECESARIO SABER:
•El
doble o duplo de un número: 2x
•El
triple de un número: 3x
•El
cuádruplo de un número: 4x
•La
mitad de un número: x/2
•Un
tercio de un número: x/3
•Un
cuarto de un número: x/4
•Un
número es proporcional a 2, 3, 4...: 2x,
3x, 4x...
•Un
número al cuadrado: x²
Tipos
de Expresiones Algebraicas
Expresión
Algebraica Racional
Es
racional cuando las variables no están afectadas por la radicación.

Expresión
Algebraica Irracional
Sonaquellas que tienen algunas de sus variables bajo un signo radical o con exponente racional no entero.

Expr.Algebraica Racional Entera
Es
racional entera cuando la indeterminada está afectada sólo por operaciones
de
suma, resta, multiplicación y potencia natural.

Expresión
Algebraica Racional Fraccionaria
Es
fraccionaria cuando la indeterminada aparece en algún denominador.
5/2+xy³-7
POLINOMIOS
Están constituidos por un conjunto finito de variables (no determinadas o desconocidas) y constantes (llamadas coeficientes)

•Monomio
: polinomio con un solo término.
•Binomio : polinomio con dos términos
•Trinomio : polinomio con tres términos
Polinomios iguales
Dos
polinomios son iguales si y sólo si los coeficientes de los términos de
igual
grado lo son.
P(x)= x4 – x3 – 2x2 + x – 2 Y Q (x)= x4 – x3 – 2x2 + x – 2
P(a)= 5x3 – x2 + x Y Q(a)= 5x3 – x2 + x
P(x) = 4x3 – 2 Y Q(x)= 4x3 – 2
Suma
de Polinomios
Se
agrupan los términos del mismo grado y se suman sus coeficientes.
P(x)
= x²-3x+5
Q(x)
= 2x²-7x-4
x² - 3x + 5 + 2x² -
7x – 4
3x²
- 10x + 1 respuesta
Propiedades
de la Suma
•Asociativa
•Conmutativa
•Existencia
de elemento neutro
•Existencia
de elemento opuesto
Resta
de Polinomios
La resta de polinomios consiste en sumar al minuendo el opuesto del sustraendo.
Q(x).3x5-6x4-5x2-7x-10
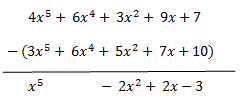
Multiplicación
de Polinomios
- Se multiplica cada monomio del primer polinomio por todos los elementos
- del segundo polinomio.Se suman los monomios del mismo grado.
P(x).2a³ - 3a²b + 4ab² - 2b³
Q(x).3a² + 4ab - 5b²
División de polinomios
Consiste en hallar uno de los factores de un producto, que recibe el nombre de cociente
dado el otro factor, llamado divisor, y el producto de ambos factores llamado dividendo.
EJEMPLO.
D(x) = 8x³ - 4x² + 2x -+7
d(x) = 2x² + x - 1
POR EL METODO DE RUFFINI

RAZONES Y PROPORCIONES
Razón
Una razón es una comparación entre dos o más cantidades. Puede expresarse
mediante una fracción. Si las cantidades a comparar son a y b, la razón entre
ellas se escribe como:
Una razón es una comparación entre dos o más cantidades. Puede expresarse
mediante una fracción. Si las cantidades a comparar son a y b, la razón entre
ellas se escribe como:
- Una razón también se puede expresar como el cociente (resultado de la división) entre el antecedente y el consecuente.

PROPORCIÓN
En una proporción del producto de los medios es igual al
producto de los extremos.Es una igualdad de dos razones
equivalentes. Se representa de la siguiente manera:
producto de los extremos.Es una igualdad de dos razones
equivalentes. Se representa de la siguiente manera:
CLASES DE PROPORCIÓN
PROPORCION DIRECTA
EJEMPLO:
Una moto que recorre a una velocidad constante, recorre 15km en 10 min
¿ Cuantos km recorrera en 25min.?
¿ Cuantos km recorrera en 25min.?
Recuerda cuando es P.Directa se realiza en CRUZ X.
KILOMETROS MINUTOS
15 ⬊ 10
x ⬈ 25
(15) (25)=(X)(10)
375=10X
10X=375
X=375/10
X= 37,5 KILOMETROS
PROPORCION INVERSA
EJEMPLO:
En una casa 8 personas arriendan un local de ropa y cada uno paga $30000
, si lo arrendaran entre 6 personas ¿ Cuanto tendria que pagar cada uno?
Recuenda que cuando es P. Inversa se realiza recto.
PERSONAS DINERO
8 ➜ 30000
6 ➔ X
(8) (30000) =(8) (x)
240000 = 8x
8x = 240000
x = 240000 / 8
x = 4000 $
PROPORCION COMPUESTA
EJEMPLO:
Hay 9 llaves abiertas durante durante 40 horas han consumido 200 litros de agua ¿ cuantos litros consumen 15 llaves durante 9 horas?
LLAVES HORAS LITROS
9 40 200
15 9 X
200/x = 9/15
200/x = 8/3
(200).(3) = (8).(x)
600 = 8x
8x = 600
x = 600/8
x = 75 LITROS
ECUACIONES
es una igualdad entre dos expresiones, denominadas miembros, separadas por el signo igual, en las que aparecen elementos conocidos, desconocidos o incógnitas, relacionados.
.
IGUALDAD
Un enunciado en el que dos expresiones (iguales o distintas) denotan el mismo objeto matemático se llama igualdad matemática
Un enunciado en el que dos expresiones (iguales o distintas) denotan el mismo objeto matemático se llama igualdad matemática

recuerda que deben ser iguales tanto en la primera variable como en la segunda. 2=2
Propiedades de la Igualdad
Propiedad Aditiva
Propiedad Multiplicativa
PROPIEDAD ADITIVA
al sumar una misma cantidad en ambos
lados, se obtiene el mismo resultado.
2x
+ 5 =
11
2x + 5 –
5 = 11 – 5
2x + 0 = 6
Propiedad Multiplicativa
Asegura que al multiplicar una
misma cantidad en ambos lados, excepto
0, se
obtiene el mismo resultado.
5 x 5 = 5 x 5
20 = 20
Propiedad
simétrica
se relaciona en poder cambiar el orden de los miembros sin
que la igualdad se altere.
EJEMPLO.
ES DECIR: 8 - 2 = X
X = 8 - 2
PASOS PARA RESOLVER ECUACIONES DE
PRIMER GRADO
PRIMER GRADO
1.Quitar paréntesis
2.Suprimir de ambos términos los miembros
iguales
3.Pasar a un miembro los términos que
contengan la incógnita, y al otro
miembro los números
4.Reducir
términos semejantes
5.Despejar la incógnita.

PASOS PARA RESOLVER LITERALES DE ECUACION.
1·Leer el problema
2·Apuntar datos
3·Escribir la ecuación
4·Resolver la ecuación
5·Interpretar el resultado
6·comprobar el resultado obtenido
EJEMPLO:Hace 4 años la edad de un tio era 9 veces que la de su
sobrino ,y dentro de 8 años sera el triple cuales son sus edades actuales.
sobrino ,y dentro de 8 años sera el triple cuales son sus edades actuales.
P: Edad actual del tio T-4=9(s-4)
S: Edad actual del sobrino T+8=3(s+8)
t-4=9s-36 ➜ t=9s-36+4
t=9h-32
t+8=3s+24 ➜ t=3s+24-8
t=3h+16
MÉTODO DE IGUALACIÓN:
9h-32 = 3h+16 p=9h-32
9h-3h = 16+32 p=3h+16
6h = 48 p=9(8)-32
h=48/6 ➜ 8 p=72-32 ➜ 40
ECUACIONES CON FRACCIONES.
EXISTEN dos tipos
de métodos:
Método de Proporciones
Método de No-Proporciones
Método
de Proporciones
Una proporción es una igualdad entre dos razones , y aparece
frecuentemente en notación fraccionaria.
Ejemplo:
5(X-1) = 3(X+2)
5X-5 = 3X+6
5X - 3X = 6+5
2X = 11
X = 11/2
METODO DE NO-PROPORCIONES
ECUACIÓN CUADRÁTICA O DE SEGUNDO
GRADO

GRADO

Con coeficientes reales tiene o bien dos soluciones reales distintas o una sola solución real multiplicidad de 2.
1) Cuando b
= 0
Se resuelve por la propiedad de primer grado
2) Cuando C =
0
ax² + bx = 0
Ecuación con trinomio cuadrado
perfecto
2) Cuando C =
0
x²-6+9 = 0
( x- 3) (x-3) = 0
x-3 = 0 x-3 = 0
x = 3 x = 3
Discriminante de la Ecuación cuadrática
Es una cierta expresión de los coeficientes de dicho polinomio que es igual
a cero si y solo siel polinomio tiene raíces múltiples en el plano complejo.
a cero si y solo siel polinomio tiene raíces múltiples en el plano complejo.
> 0 ➜ TIENE DOS SOLUCIONES REALES DISTINTAS
= 0 ➜ TIENE UNA SOLUCIÓN DOBLE
< 0 ➜ NO TIENE SOLUCIÓN



EJERCICIO GENERAL
ax²-3x-4 =0
INTERVALOS Y DESIGUALAIONES
INTERVALOS:son
subconjuntos de los números reales que se pueden
representar gráficamente en la
recta numérica.
INTERVALO ABIERTO.
no a los puntos finales.
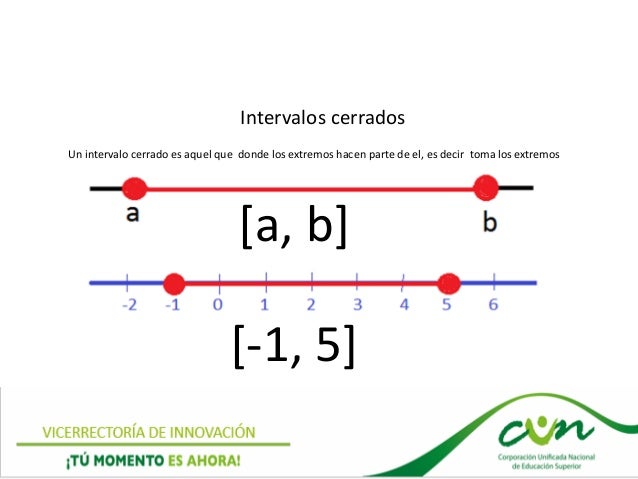
INTERVALO CERRADO.
Conjunto que contiene en sí sus puntos extremos y todos los números apropiados.

INTERVALO SEMI ABIERTO.
Es el conjunto de números reales comprendidos entre dos determinados: a y b,
llamados extremos delintervalo.
INTERVALO SEMI CERRADO.
INTERVALOS INDETERMINADOS

MAYOR O IGUAL QUE.
MENOR O IGUAL QUE.
Recuerda que el infinito nunca se incluye dentro de unintervalo y además nunca se
escribe en la desigualdad.
Desigualdades
Es una relación de orden que se da entre dos valores cuando éstos son distintos (en caso de
ser iguales, lo que se tiene es una igualdad).

INECUACIONES
en la
que hay una o mas cantidades desconocidas (incógnitas) y que sólo se
verifica
para determinados valores de las incógnitas.
EJEMPLO.
x <
2 à ( - oo
, 2 )
x ≥ - 4 à
[ - 4 , + oo
)
INECUACIONES CON UNA INCOGNITA
Intervienen
incógnitas o valores desconocidos
•EJEMPLO.
•x < 7 x es siempre MENOR que 7
•x ≤ -8 x es MENOR o IGUAL que -8
•x > 1 x es siempre MAYOR que 1
•x ≥ -4 x es MAYOR o IGUAL que -4
INECUACIONES LINEALES.
Es una desigualdad en la que intervienen una o más incógnitas, y es de primer grado
cuando la potencias más grande con la que se encuentra la incógnita es igual a uno.

INECUACIONES CUADRATICAS.
variabltiene exponente 2 y es en su forma general de una de las formas.
ax2 + bx + c ≥ 0
EJERCICIO GENERAL
7x2 + 21x − 28 < 0
x2 +3x − 4 < 0
x2 +3x − 4 = 0
P(−6) = (−6)2 +3 · (−6)− 4 > 0
P(0) = 02 +3 · 0 − 4 < 0
P(3) = 32 +3 · 3 − 4 > 0
(−4, 1)
EJERCICIO 2
P(−3) = 4 · (−3)2 − 16 > 0
P(0) = 4 · 0 2 − 16 < 0
P(3) = 4 · 3 2 − 16 > 0
EJERCICIO 3

Por lo que el conjunto solución de  es
es ![$[\,0,4\, ];$](https://tecdigital.tec.ac.cr/revistamatematica/cursos-linea/MATEGENERAL/t3-inecuaciones/inecuaciones-julioetall/img234.gif) o sea : S =
o sea : S = 
SUCESIONES







SUCESIONES
Es un conjunto ordenado de objetos matemáticos,a números. Cada uno de ellos es denominado término de la sucesión y al número de elementos
SU NOTACION:
TIPOS DE SUCESIONES:
SUCESION ARITMETICA:
Es una sucesión de números tales que la diferencia de dos términos sucesivos cualesquiera de la secuencia es una constante.
| 1, 4, 7, 10, 13, 16, 19, 22, 25, ... |
Esta sucesión tiene una diferencia de 3 entre cada dos términos.
La regla es xn = 3n-2
SUCESION GEOMRTRICA:
En una sucesión geométrica cada término se calcula multiplicando el anterior por un número fijo.
| 3, 9, 27, 81, 243, 729, 2187, ... |
Esta sucesión tiene un factor 3 entre cada dos términos.
La regla es xn = 3n
La regla es xn = 3n
EJEMPLOS DE SUCESIONES:
{20, 25, 30, 35, ...} también es una sucesión infinita
{4, 3, 2, 1} va de 4 a 1 hacia atrás
{a, b, c, d, e} es la sucesión de las 5 primeras letras en order alfabético
{a, l, f, r, e, d, o} es la sucesión de las letras en el nombre "alfredo"
SU ORDEN:
Una sucesión es muy parecida a un conjunto, pero con los términos en orden (y el mismo valor sí puede aparecer muchas veces).
SU REGLA:
Sigue una regla que te dice cómo calcular el valor de cada término.
SUCESIONES ESPECIALES:
Números triangulares
| 1, 3, 6, 10, 15, 21, 28, 36, 45, ... |
se genera a partir de una pauta de puntos en un triángulo.
Pero es más fácil usar la regla
xn = n(n+1)/2
Ejemplo:
- El quinto número triangular es x5 = 5(5+1)/2 = 15,
- y el sexto es x6 = 6(6+1)/2 = 21
Números cuadrados
| 1, 4, 9, 16, 25, 36, 49, 64, 81, ... |
El siguiente número se calcula elevando al cuadrado su posición.
La regla es xn = n2
NUMEROS CUBICOS
| 1, 8, 27, 64, 125, 216, 343, 512, 729, ... |
El siguiente número se calcula elevando al cubo su posición.
La regla es xn = n3
NUNEMORS DE FIBONACCI
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... |
El siguiente número se calcula sumando los dos que están antes de él.
El 2 se calcula sumando los dos delante de él (1+1)
El 21 se calcula sumando los dos delante de él (8+13)
La regla es xn = xn-1 + xn-2
Esta regla es interesante porque depende de los valores de los términos anteriores.
Por ejemplo el 6º término se calcularía así:
x6 = x6-1 + x6-2 = x5 + x4 = 5 + 3 = 8
EJERCICIO GENERAl

EJEMPLO 2

EJEMPLO 3












 )
)